2021年03月20日 - WebVR・Three.js

GLSLでジュリア集合

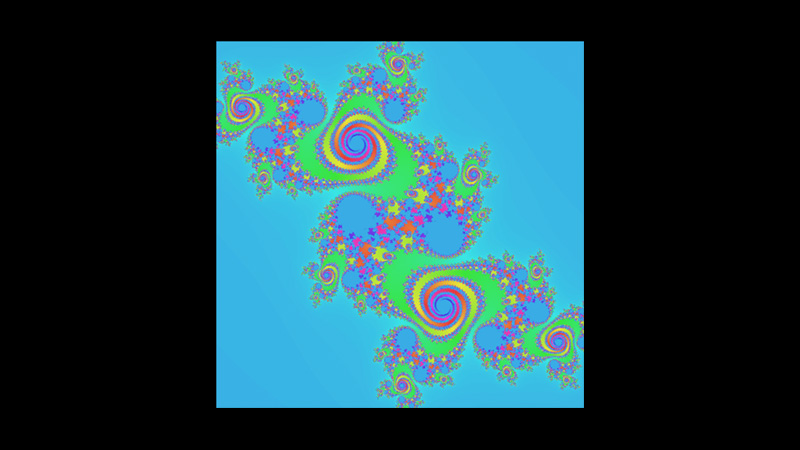
「WebGLでシェーダ（GLSL）入門」に続き「ジュリア集合-wgld.org」を参考に、GLSLでジュリア集合を試しました。

GLSLでジュリア集合

ジュリア集合はフラクタル図形の一つです。フラクタル図形は、フランスの数学者ブノワ・マンデルブローが導入した幾何学の概念で、大雑把にいうと同じような図形が繰り返し現れる図形のことです。フラクタル図形には他にマンデルブロ集合やコッホ曲線、シェルピンスキー曲線などがあります。

ジュリア集合は、漸化式と呼ばれる、ある答えを導き出すためのルールを表現した数式を使用して実装します。

● script.jsの読み込み

script.jsは「WebGLでシェーダ（GLSL）入門」と同じものを使用します。

<script src="js/script.js" type="module"></script>

● glsl.js

const vertexShader =`
	attribute vec3 position;

	void main(void){
		gl_Position = vec4(position,1.0);
	}
`;

const fragmentShader =`
	precision mediump float;

	uniform float time;
	uniform vec2 mouse;
	uniform vec2 resolution;

	//HSVカラー生成
	vec3 hsv(float h,float s,float v){
		vec4 t = vec4(1.0,2.0/3.0,1.0/3.0,3.0);
		vec3 p = abs(fract(vec3(h) + t.xyz) * 6.0 - vec3(t.w));
		return v * mix(vec3(t.x),clamp(p - vec3(t.x),0.0,1.0),s);
	}

	void main(void){

		//フラグメント座標の正規化
		vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x,resolution.y);

		//ジュリア集合
		int j = 0;
		vec2 x = vec2(-0.1,0.654);
		vec2 y = vec2(0.005,0.0);
		vec2 z = p;

		//漸化式の繰り返し
		for(int i = 0; i < 360; i++){
			j++;
			if(length(z) > 2.0){
				break;
			}
			z = vec2(z.x * z.x - z.y * z.y, 2.0 * z.x * z.y) + x + y;
		}

		//カラーの出力
		float h = abs(mod(200.0 - float(j),360.0) / 360.0);
		vec3 rgb = hsv(h,0.75,0.9);

		gl_FragColor = vec4(rgb,1.0);
	}
`;

export { vertexShader, fragmentShader };

完成したデモになります。GLSLでジュリア集合を試しました。